Casual Inference Data analysis and other apocrypha
Do better QA with just a little bit of Bayesian statistics: Beta-Binomial analysis in Python
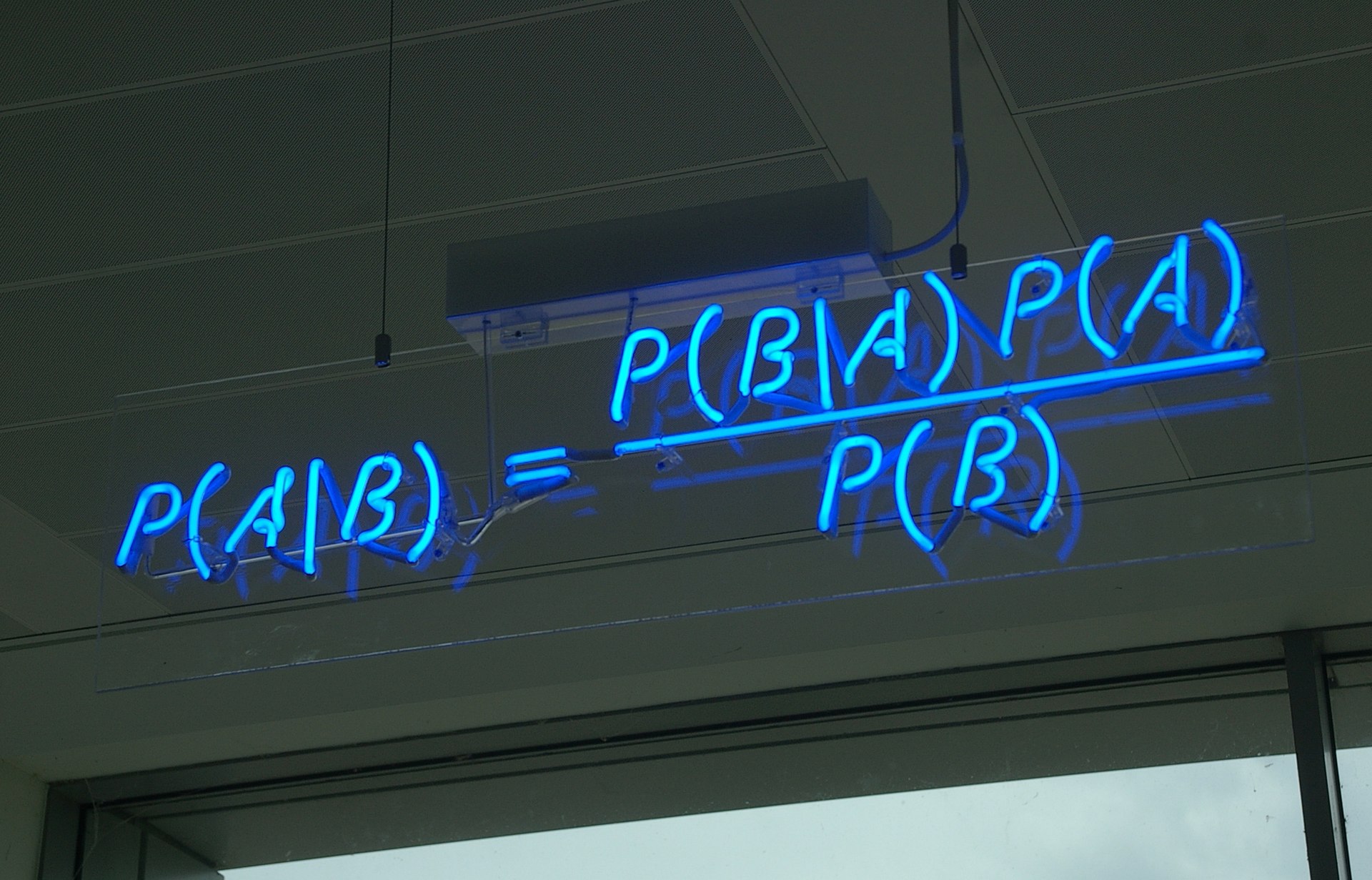
Do better QA with just a little bit of Bayesian statistics
Whatever product you’re making - software, drugs, lightbulbs, AI chat experiences, croissants, pulse oximeters, you name it - you eventually will need to figure out whether your product is good enough. This takes many forms, such as:
- Drugs need to provide the advertised effect, without major side effects.
- Lightbulbs need to last as many hours as they claim.
- AI responses need to successfully provide answers to user queries, ideally close to 100% of the time.
This process of measuring the good-enough-ness of the product is commonly called Quality Assurance (QA) or perhaps Quality Control (QC). But quality is a famously tricky thing to understand. 1
General methods for QA of a product:
- Direct inspection - the most common, and the one we talk about here. Have a person or automated system look at it, and evaluate whether it is good enough
- Study the effects of the products - A/B tests, clinical trials, measure whether it does what you want
- Simulated environment - Cross-validation, physical device testing, unit testing
Direct inspection is usually the first thing you try, especially if you’re not sure what you’re looking for yet. The problem is that this this is usually expensive, and so we usually can’t inspect every outgoing item; we can only inspect a sample. We need to use the sample to decide whether this batch is okay to ship or not; we will base this decision on whether the failure rate for the whole batch is greater than the highest acceptable failure rate
Okay so you’ve got the basics down: you know your unit, you have your evaluation measure (binary or real), you have a batch, you have a target failure rate
At this point, you’ve decided on:
- What the unit of evaluation is (one lightbulb, one chat session, etc)
- How you will measure whether it is meets your standards (manual inspection, automated measurement, etc)
- The size of the sample you’re going to collect, $n$
- The highest acceptable failure rate, $\mu^{*}$
You collect $y = 40$ out of $n = 1000?$ failures. is that okay? It seems pretty close, how sure are we that the rest of the batch is safe?
Bayesics: Beta Binomial analysis of the failure rate
Bayesian analysis is a little three-step dance that goes like this:
- Pick a prior
- Observe the data
- Update the prior to get the posterior. Use the posterior to calculate the probability $\mu < 5\%$.
The beta distribution is a relatively flexible distribution over the interval $[0, 1]$.
Conjugate prior:mn
$\underbrace{\mu}{\text{Our prior on the rate}} \sim \underbrace{Beta(\alpha_0, \beta_0)}{\text{is a Beta distribution with params } \alpha_0, \beta_0}$
You can interpret the prior parameters as “hypothetical data” that summarizes your beliefs about the rate.
Posterior:
$\underbrace{\mu \mid y, n}{\text{The posterior of the rate given the data}} \sim \underbrace{Beta(\alpha_0 + y, \beta_0 + N - y)}{\text{is given by this beta distribution}}$
That was kind of a lot, so lets recap:
- You’ve collected data $y$ and $n$
- Select the prior parameters $\alpha_0, \beta_0$
- Update the parameters with the data to get the posterior, which will have parameters $\alpha = \alpha_0 + y, \beta = \beta_0 + (n - y)$
- Infer the probability that the failure rate is less than the target, calculating $\mathbb{P}(\mu < \mu^*)$
Doing the analysis for our sample
We’ll use the implementation of the beta distribution found in scipy.
from scipy.stats import beta
y = 40
n = 1000
a_0 = 1./3
b_0 = 1./3
posterior = beta(a_0 + y, b_0 + n - y)
n_simulations = 100000
posterior_samples = posterior.rvs(n_simulations)
print('Monte carlo estimate of P(Rate) < 5%: ', sum(posterior_samples < .05) / len(posterior_samples))
print('CDF(5%) = ', posterior.cdf(.05))
Digression: Picking a prior
“Flat” or “uninformative” priors
If you’re just getting started, the recommended prior of 1/3, 1/3 is probably good enough. But using statistics responsibly does mean thinking through all the details of your method, so pinky promise me you’ll come back and read this sometime, okay?
A commonly used prior is … . If you think more than one prior, applies, the safest thing is to try all of them and see how much they change your result.
| Values of $\alpha, \beta$ | Fancy name | Notes |
|---|---|---|
| $(0, 0)$ | Haldane | Improper prior |
| $(1, 1)$ | Uniform | Assigns equal value to all possibilities |
| $(\frac{1}{2}, \frac{1}{2})$ | Jeffreys | Jeffrey’s rule reference prior |
| $(\frac{1}{3}, \frac{1}{3})$ | Neutral | Ensures median |
Kerman paragraph
See Kerman 2011.
Informative priors based on expert knowledge
Certain posteriors are just not possible, and we should represent this fact in our prior
Extrapolating to the whole batch: Predictive simulation with the Beta-Binomial model
We often want to know how many defective are in the whole batch for planning (maybe we make a warantee for customers, or have support centers which need to be staffed, or expect other adverse effects for each one shipped)
https://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.betabinom.html
What’s the smallest sample I could collect?
Sample size -> Precision is the real thing. Simulation?
Where to learn more
Gelman
Endnotes
1: Zen and the Art of Motorcycle Maintenance explores this in a way which I found to be amusing, if not exactly sound philosophical material.
Appendix: A shortcut when defects are rare events: The rule of three
compare with beta interval using jeffrey’s prior
Written on th, by Louis Cialdella